高数是什么?o.O

第七章重积分

二重积分

大概是：在面积的基础上计算体积

$\iint f\left(x,y\right)d\sigma$

常见方法：直角坐标系（x型,y型），极坐标系，任意坐标系

直角坐标系（x型）： $\iint f\left(x,y\right)dxdy=\int_a^bdx\int_{g1(x)}^{g2(x)}f(x,y)dy$
直角坐标系（y型）： $\iint f\left(x,y\right)dxdy=\int_c^ddy\int_{\psi1(y)}^{\psi2(y)}f(x,y)dx$
极坐标系： $\iint f\left(x,y\right)dxdy=\int_{\theta1}^{\theta2}d\theta\int_{r1(\theta)}^{r2(\theta)}f(r\cos\theta,r\sin\theta)rdr$
任意坐标系： $\iint f\left(x,y\right)dxdy=\iint f(x(u,v),y(u,v))\left|J\right|dudv$
其中 $\left|J\right|=\begin{vmatrix}\frac{\partial x}{\partial u}&\frac{\partial x}{\partial v}\\\frac{\partial y}{\partial u}&\frac{\partial y}{\partial v}\end{vmatrix}$

常用性质：奇偶对称性
note：
转化为极坐标时常涉及高次cosx，sinx关于x的积分。
$\int_0^\frac\pi2\sin^{2k}\left(x\right)dx=\int_0^\frac\pi2\cos^{2k}\left(x\right)dx=\frac{(2k-1)!!}{(2k)!!}\times\frac{\mathrm\pi}2$
$\int_0^\frac\pi2\sin^{2k+1}\left(x\right)dx=\int_0^\frac\pi2\cos^{2k+1}\left(x\right)dx=\frac{(2k)!!}{(2k+1)!!}$
当积分区域为椭圆时，令 $x=ar\cos\theta,y=br\sin\theta$ , 则 $\iint f(x,y)dxdy=\int_\alpha^\beta d\theta\int_0^\lambda f(ar\cos\theta,br\sin\theta)abrdr$
当积分不太好计算时，可以尝试交换积分顺序（注意上下限的变化）

三重积分

大概是：在体积的基础上计算质量

$\iiint f\left(x,y,z\right)dV$

常见方法：直角坐标系（投影法，截面法），柱坐标系(投影法，截面法)，球坐标系，任意坐标系

直角坐标系（投影法）： $\iiint f(x,y,z)dxdydz=\iint dxdy\int_{z1(x,y)}^{z2(x,y)}f(x,y,z)dz$
直角坐标系（截面法）： $\iiint f(x,y,z)dxdydz=\int_a^bdz\iint f(x,y,z)dxdy$
柱坐标系(投影法)： $\iiint f(x,y,z)dxdydz=\iint rdrd\theta\int_{\psi(r,\theta)}^{\nu(r,\theta)}f(r\cos\theta,r\sin\theta,z)dz$
柱坐标系（截面法）： $\iiint f(x,y,z)dxdydz=\int_\alpha^\beta d\theta\iint f(r\cos\theta,r\sin\theta,z)rdrdz$
球坐标系： $\iiint f(x,y,z)dxdydz=\int_\alpha^\beta d\theta\int_\omega^\gamma\sin\psi d\psi\int_{g1(\psi,\theta)}^{g2(\psi,\theta)}f(\rho\sin\psi\cos\theta,\rho\sin\psi\sin\theta,\rho\cos\psi)\rho^2d\rho$
其中， $\theta$ 是在xy平面上与x轴的夹角（与x轴的正半轴重合记为0）， $\psi$ 是截面上与z轴的夹角（与z的正半轴重合记为0）
任意坐标系： $\iiint f(x,y,z)dxdydz=\iiint f(x(u,v,w),y(u,v,w),z(u,v,w))\left|J\right|dudvdw$
其中， $\left|J\right|=\begin{vmatrix}\frac{\partial x}{\partial u}&\frac{\partial x}{\partial v}&\frac{\partial x}{\partial w}\\\frac{\partial y}{\partial u}&\frac{\partial y}{\partial v}&\frac{\partial y}{\partial w}\\\frac{\partial z}{\partial u}&\frac{\partial z}{\partial v}&\frac{\partial z}{\partial w}\end{vmatrix}$

常用性质：奇偶对称性（假设积分区域关于Oxy平面对称，则若f(x,y,z)关于z是奇函数，积分为0）
note：当积分区域为椭球时，令 $x=ar\sin\psi\cos\theta,y=br\sin\psi\sin\theta,z=cr\cos\psi$ ，则 $\iiint f(x,y,z)dxdydz=\int_\alpha^\beta d\theta\int_\nu^\kappa\sin\psi d\psi\int_0^\lambda f(ar\sin\psi\cos\theta,br\sin\psi\sin\theta,cr\cos\psi)abcr^2dr$

重积分的应用举例

求曲面面积： $S=\iint\sqrt{1+{f^2}_x(x,y)+{f^2}_y(x,y)}d\sigma$
其中， $z=f(x,y)$ ， $\sigma$ 是投影面积。
求质心： $x_0=\frac{\iiint x\rho(x,y,z)dV}m,y_0=\frac{\iiint y\rho(x,y,z)dV}m,z_0=\frac{\iiint z\rho(x,y,z)dV}m$
求转动惯量： $J_o=\iiint(x^2+y^2+z^2)\rho(x,y,z)dV$ (到原点的转动惯量)
求引力： $F=k\iiint\frac{m0\rho(x,y,z)dV}{r^2}\frac{\boldsymbol r}r$

第八章曲线积分与曲面积分

曲线积分

第一型曲线积分：化曲为直
$\int_Lf(x,y)ds=\int_a^bf(x,y(x))\sqrt{1+\left[y'(x)\right]^2}dx$
$\int_Lf(x,y)ds=\int_\alpha^\beta f(\varphi(t),\psi(t))\sqrt{\left[\varphi'(t)\right]^2+\left[\psi'(t)\right]^2}dt$
$\int_Lf(x,y,z)ds=\int_\alpha^\beta f(\varphi(t),\psi(t),\omega(t))\sqrt{\left[\varphi'(t)\right]^2+\left[\psi'(t)\right]^2+\left[\omega'(t)\right]^2}dt$

第二型曲线积分：统一投影直线

非封闭曲线：

$\int\boldsymbol F(x,y,z)\boldsymbol\cdot d\boldsymbol r=\int Pdx+Qdy+Rdz$

$\int_{AB}P(x,y)dx+Q(x,y)dy=\int_a^b\left[P(x,y(x))+Q(x,y(x))y'(x)\right]dx$
$\int_{AB}P(x,y)dx+Q(x,y)dy=\int_\alpha^\beta\left[P(\varphi(t),\psi(t))\varphi'(t)+Q(\varphi(t),\psi(t))\psi'(t)\right]dt$

封闭曲线：
格林公式(连续可导)
曲线正方向：内顺外逆

$\oint Pdx+Qdy=\iint(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy$

斯托克斯公式（本质格林公式）

$\oint Pdx+Qdy+Rdz=\iint\begin{vmatrix}dydz&dzdx&dxdy\\\frac\partial{\partial x}&\frac\partial{\partial y}&\frac\partial{\partial z}\\P&Q&R\end{vmatrix}$

也可写成

$\oint Pdx+Qdy+Rdz=\iint\begin{vmatrix}\cos\alpha&\cos\beta&\cos\gamma\\\frac\partial{\partial x}&\frac\partial{\partial y}&\frac\partial{\partial z}\\P&Q&R\end{vmatrix}dS$

其中，L的正向与S的正向构成右手系。
且 $\left(\cos\alpha,\cos\beta,\cos\gamma\right)$ 是平面S的单位法向量

与路径无关的条件

$\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}$
$Pdx+Qdy=du(x,y)$
du(x,y)求法：

观察法 $Pdx+Qdy=f(x)dx+\left[g(x,y)dx+u(x,y)dy\right]+k(y)dy=du$
特殊路径法

曲面积分

第一型曲面积分：化曲面为平面
$\iint f(x,y,z)dS=\iint f(x,y,z(x,y))\sqrt{1+z_x^2+z_y^2}d\sigma$
$\iint f(x,y,z)dS=\iint f(x(u,v),y(u,v),z(u,v))\sqrt{EG-F^2}dudv$
其中， ${\boldsymbol r}_u=\begin{pmatrix}x_u\\y_u\\z_u\end{pmatrix}\;,\;{\boldsymbol r}_v=\begin{pmatrix}x_v\\y_v\\z_v\end{pmatrix}\;,\;E=\left|{\boldsymbol r}_{\mathbf u}\right|^2\;,\;G=\left|{\boldsymbol r}_{\boldsymbol v}\right|^2\;,\;F={\boldsymbol r}_{\mathbf u}\boldsymbol\cdot\boldsymbol\;{\boldsymbol r}_{\mathbf v}\\$

第二型曲面积分：统一投影平面

非封闭曲面：

$\iint\boldsymbol F\boldsymbol\cdot\boldsymbol ndS=\iint Pdydz+Qdzdx+Rdxdy$

曲面法向量：
$F(x,y,z)=0\;,\boldsymbol\;\boldsymbol n=\nabla F(x,y,z)=(F_x\;,F_y,F_z)\;$
投影在xy平面：
$\iint Pdydz+Qdzdx+Rdxdy=\pm\left[\iint P(x,y,z(x,y))(F_x)+Q(x,y,z(x,y))(F_y)+R(x,y,z(x,y))(F_z)\right]dxdy$
根据曲线S的指向定正负，若指向z轴正方向，则取+，否则取—。
广义坐标变换：
$\iint Pdydz+Qdzdx+Rdxdy=\left[\pm\iint P(x(u,v),y(u,v),z(u,v))\frac{\partial\left(y,z\right)}{\partial\left(u,v\right)}\pm\iint Q(x(u,v),y(u,v),z(u,v))\frac{\partial\left(z,x\right)}{\partial\left(u,v\right)}\pm\iint R(x(u,v),y(u,v),z(u,v))\frac{\partial\left(x,y\right)}{\partial\left(u,v\right)}\right]dudv$

封闭曲面：
高斯公式（连续可导）

$\iint Pdydz+Qdzdx+Rdxdy=\iiint(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z})dV$

即， $\iint\boldsymbol F\boldsymbol\cdot\boldsymbol ndS=\iiint div\boldsymbol FdV$ ，div为散度

note：若曲面S在某一坐标平面上投影为0 ，则相应积分为0

第九章常微分方程

一阶常微分方程

分离变量法：

$\frac{dy}{dx}=f(x)\cdot g(y)$

可化为变量分离方程的几类方程：
形式：
(1) $\frac{dy}{dx}=f(ax+by+c)$ 令z=ax+by+c，则 $\frac{dz}{dx}=a+b\frac{dy}{dx}=a+bf(z)$ ，即 $\frac{dz}{a+bf(z)}=dx$
(2) $\frac{dy}{dx}=f(x,y)$ ，其中，f(x,y) 是齐次函数，令 $u\;=\;\frac yx,\;$ 则 $y\;=\;ux,\;y'=u+xu'=h(u),\;\frac{du}{dx}=\frac{h(u)-u}x$
(3) $\frac{dy}{dx}=f(\frac{a_1x+b_1y+c_1}{a_2x+b_2y+c_2})$ ,

$a_1x+b_1y\neq k(a_2x+b_2y),$ 联立方程组 $\left\{\begin{array}{l}a_1x+b_1y+c_1=0\\a_2x+b_2y+c_2=0\end{array}\right.$ 解得 $(x_0,y_0)$ 令 $u=x-x_0,v=y-y_0,\;$ 则 $\frac{dv}{du}=f(\frac{a_1u+b_1v}{a_2u+b_2v}),\;$ 转化为情况二
$a_1x+b_1y=k(a_2x+b_2y)$ ，则令 $z=a_1x+b_1y,\;z'=a_1+b_1y'=a_1+b_1h(z)$

一阶线性方程

$\frac{dy}{dx}+P(x)y=Q(x)$

(1) $Q(x)=0$ : $\frac{dy}{dx}=-P(x)y$
(2) $Q(x)\neq0$ :

常数变易法：先得到左侧齐次方程的通解 $y=C\varphi(x)$ ，再将其中的C替换为C(x),将 $y=C(x)\varphi(x)$ 代入原方程得， $C'(x)\varphi(x)=Q(x)$ , 求得C(x)
伯努利方程：
$\frac{dy}{dx}+P(x)y=Q(x)y^\alpha$ , 令 $z=y^{1-\alpha},\;\frac1{1-\alpha}\frac{dz}{dx}+P(x)z=Q(x)$

全微分方程

$\frac{dy}{dx}=\frac{-P(x,y)}{Q(x,y)}$

(1)观察法：上式可写作 $P(x,y)dx+Q(x,y)dy=0$ , 令 $du(x,y)=P(x,y)dx+Q(x,y)dy=0,$ 则 $u(x)=C$
(2)积分因子法： $M(x,y)dx+N(x,y)dy=0$
只关于x的函数 $F(x)=(\frac{\partial M}{\partial y}-\frac{\partial N}{\partial x})/N(x,y)$ 则积分因子 $\mu(x)=e^{\int F(x)dx}$
只关于y的函数 $G(y)=(\frac{\partial N}{\partial x}-\frac{\partial M}{\partial y})/M(x,y)$ 则积分因子 $\mu(y)=e^{\int G(y)dy}$

高阶方程

（1）降阶法：

不显含y的方程：
$F(x,y',y'')=0,\;z=y',\;F(x,z,z')=0$
不显含x的方程：
$F(y,y',y'')=0,\;p=y',\;F(y,p,p\frac{dp}{dy})=0$ 得到 $G(p,y)=G(\frac{dy}{dx},y)=0$

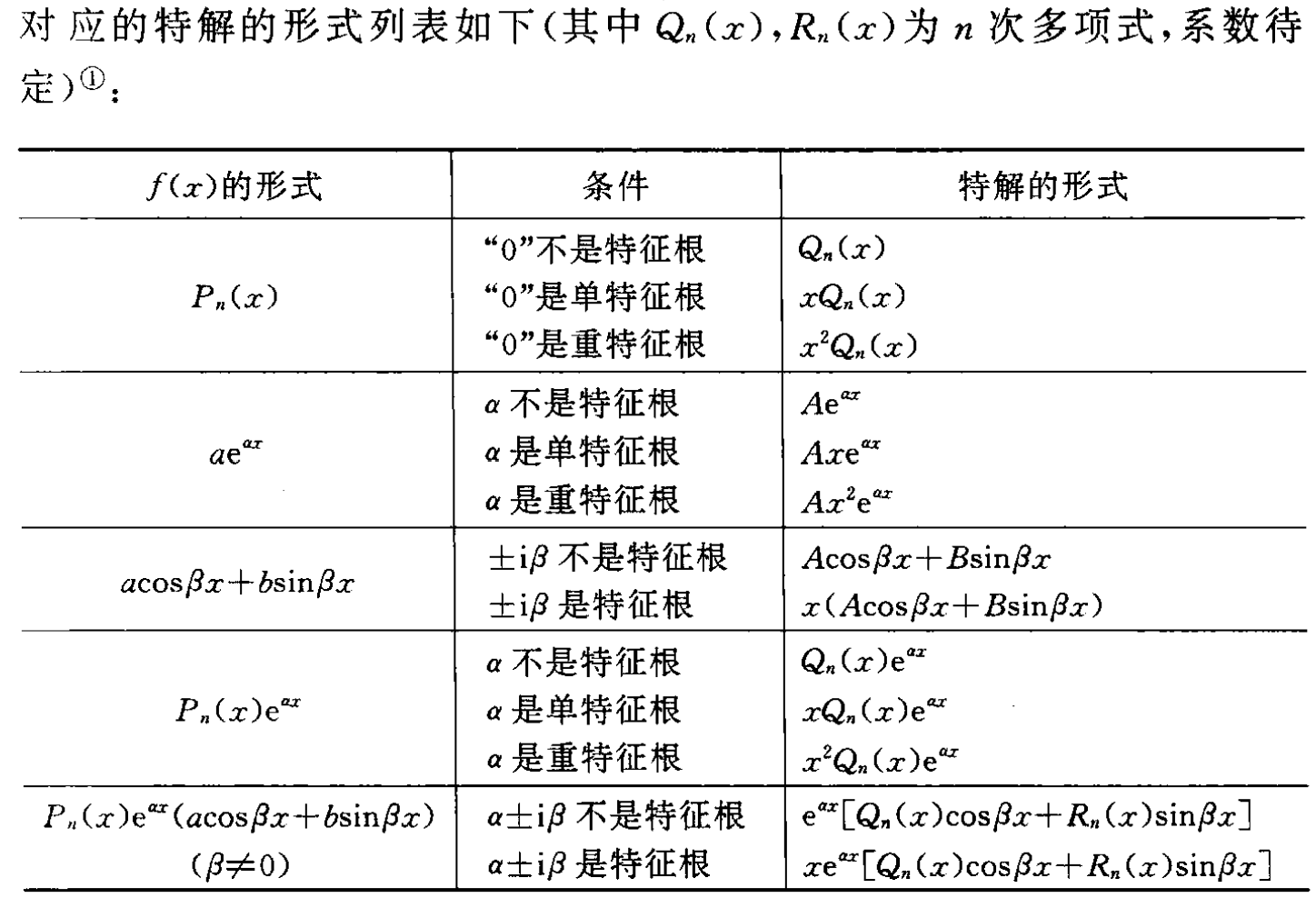
(2) 特征根+待定系数法：（适用于常系数微分方程）

$y''+py'+qy=f(x)$

非齐次线性方程的解=齐次方程的通解+特解
通解：
当特征解为实数时：
$\left\{\begin{array}{l}C_1e^{\lambda_1x}+C_2e^{\lambda_2x}+...,\;\lambda_i\neq\lambda_j(i\neq j)\\(C_1+C_2x+C_3x^2+...C_mx^{m-1})e^{\lambda_1x},\;\lambda_1=\lambda_2=...=\lambda_m\end{array}\right.\\$
当特征解为m重共轭复根 $\lambda_{1,2}=\alpha\pm i\beta$ 时：
$e^{\alpha x}(C_1\cos\beta x+C_2\sin\beta x+C_3x\cos\beta x+C_4x\sin\beta x+...+C_nx^{m-1}\cos\beta x+C_nx^{m-1}\sin\beta x)$
特解：

(3) 常数变易法：
先求齐次方程对应通解： $y=C\varphi_1(x)+C\varphi_2(x)$
接着， $\left\{\begin{array}{l}C_1'(x)\varphi_1(x)+C_2'(x)\varphi_2(x)=0\\C_1'(x)\varphi_1'(x)+C_2'(x)\varphi_2'(x)=f(x)\end{array}\right.$
$y=C_1(x)\varphi_1(x)+C_2(x)\varphi_2(x)$ 即为非齐次方程的解

(4)消元法:(适用于常系数线性微分方程组)
原理：将y用 $\frac{dx}{dt}$ 或x表示，形成x的常系数微分方程

微分方程解的存在和唯一性定理

初值问题与积分方程 $y=y_0+\int_{x_0}^xf(x,y)dx$ 等价
初值问题在区间 $x\in\lbrack x_0-h,x_0+h\rbrack$ 有一个解， $h=min(a,b/M),\;M=max\{\left|f(x,y)\right|(x,y)\in R\}$
皮卡序列： $y_n(x)=y_0+\int_{x_0}^xf(x,y_{n-1}(x))dx,\;x\in\lbrack x_0-h,x_0+h\rbrack,\;n=1,2...$

第十章无穷级数

只含n的级数

收敛定义： $S_n=\sum_{k=1}^na_k$ 部分和有极限S
由定义可延伸出判断级数发散的两种方法：

当n趋近于无穷时， $a_n$ 不等于零，级数发散
$\left|\sum_{k=n+1}^{n+p}a_k\right|\;\;\geq l\;(l>0)$ （由此可判断 $\sum_{n=1}^{\infty}\frac1n$ 发散）

正项级数的收敛判别法：

比较判别： $u_n\leq v_{n\;\;\;}$ ，若 ${\textstyle\sum_{n=1}^\infty}u_n$ 发散则 ${\textstyle\sum_{n=1}^\infty}v_n$ 发散 , 若 ${\textstyle\sum_{n=1}^\infty}v_n$ 收敛，则 ${\textstyle\sum_{n=1}^\infty}u_n$ 收敛
比值判别： $\lim_{n\rightarrow\infty}\frac{u_n}{v_n}=h$
(1) h=0,若 ${\textstyle\sum_{n=1}^\infty}v_n$ 收敛，则 ${\textstyle\sum_{n=1}^\infty}u_n$ 收敛
（2） $h=\infty$ ，若 ${\textstyle\sum_{n=1}^\infty}v_n$ 发散，则 ${\textstyle\sum_{n=1}^\infty}u_n$ 发散
（3） $0<h<\infty$ , 则 ${\textstyle\sum_{n=1}^\infty}v_n$ 与 ${\textstyle\sum_{n=1}^\infty}u_n$ 敛散性相同
达朗贝尔判别： $\lim_{n\rightarrow\infty}\frac{u_{n+1}}{u_n}=l$ （1）l<1,收敛（2）l>1,发散（3）l=1,不定
柯西判别： $\lim_{n\rightarrow\infty}\sqrt[n]{u_n}=l$ （1）l<1,收敛（2）l>1,发散（3）l=1,不定
积分判别： $u_n=f(n)$ ， f(x)单调下降且非负，则 ${\textstyle\sum_{n=1}^\infty}u_n$ 收敛 $\leftrightarrow\int_1^\infty f(x)dx$ 收敛

交错级数的收敛判别法：
莱布尼茨判别法：
$(1)\;\left|u_n\right|\geq\left|u_{n+1}\right|\\(2)\;\lim_{n\rightarrow\infty}\left|u_n\right|=0$
${\textstyle\sum_{k=1}^\infty}a_kb_k$ 类型级数收敛判别法：

迪利克雷判别：序列 $\{a_k\}$ 单调且 $\lim_{k\rightarrow\infty}a_k=0$ , 又 $\left|{\textstyle\sum_{k=1}^nb_k}\right|\leq M$
阿贝尔判别：序列 $\{a_k\}$ 单调且 $\left|\lim_{k\rightarrow\infty}\{a_k\}\right|\leq M$ ，又 ${\textstyle\sum_{k=1}^\infty}b_k$ 收敛

任意项级数收敛判别法：
绝对收敛则一定收敛：若 ${\textstyle\sum_{k=1}^\infty}\left|u_k\right|$ 收敛，则 ${\textstyle\sum_{k=1}^\infty}u_k$ 收敛
note：
等比级数： $S_{n\;}=\frac{a(1-q^n)}{1-q}->\left\{\begin{array}{l}\frac a{1-q},\left|q\right|<1\\\infty,\left|q\right|>1\end{array}\right.$
p级数： ${\textstyle\sum_{n=1}^\infty}\frac1{n^p}$ ,当 $p\leq1$ 时发散，p>1时收敛
级数 ${\textstyle \sum_{n=1}^{\infty }} \frac{\sin n\varphi }{n^{p} }$ ，p>1时绝对收敛， $0\le p\le1$ 时条件收敛

函数级数

函数序列一致收敛:存在 $N(\varepsilon)$ ,只要 $n>N(\varepsilon)$ ，总有 $\left|f_n(x)-f(x)\right|<\varepsilon$ ，其中， $f(x)=\lim_{n\rightarrow\infty}f_n(x)$
由定义可延伸出判断函数序列不一致收敛的方法：
存在点列 $x_n\in X$ 使得 $\left|f_n(x_n)-f(x_n)\right|\geq l\;(l>0)$ ，或 $\left[f_n(x_n)-f(x_n)\right]\rightarrow k\neq0\;(n\rightarrow\infty)$
函数项级数一致收敛： $S_n(x)={\textstyle\sum_{k=1}^n}u_k(x)$ 在X上一致收敛，则级数 ${\textstyle\sum_{n=1}^\infty}u_n(x)$ 在X上一致收敛
类比只含n级数可延伸出判断函数项级数不一致收敛的方法：

一般项 $u_n(x)$ 不一致趋于0，即存在点列 $x_n\in X$ 使得 $\lim_{n\rightarrow\infty}\left|u_n(x)\right|\neq0$
$\left|\sum_{k=n+1}^{n+p}u_k(x)\right|\;\;\geq l\;(l>0)$

函数级数一致收敛性判别法：

强级数判别： $\left|u_n(x)\right|\leq a_n$ , ${\textstyle\sum_{n=1}^\infty}a_n$ 收敛，则该级数在X上一致收敛
有的时候可以通过求导获取 $u_n(x)$ 的极大值，极大值收敛也可证明该级数收敛
迪利克雷判别： $u_n(x)=a_n(x)b_n(x)$
（1） $\{a_n(x)\}$ 对n单调，且 $\{a_n(x)\}$ 在X上一致收敛于0
（2）部分和一致有界 $\left|{\textstyle\sum_{k=1}^n}b_k(x)\right|\leq M$
阿贝尔判别：
（1） $\{a_n(x)\}$ 对n单调，且 $\{a_n(x)\}$ 在X上一致有界
（2） ${\textstyle\sum_{n=1}^\infty}b_n(x)$ 在X上一致收敛

一致收敛性质

$\lim_{x \to x_0} {\textstyle \sum_{n=1}^{\infty }} u_n(x)= {\textstyle \sum_{n=1}^{\infty }} \lim_{x \to x_0} u_n(x)$ (条件： ${\textstyle \sum_{n=1}^{\infty }} u_n(x)$ 一致收敛且每一项都连续)
$\int_{a}^{b} {\textstyle \sum_{k=1}^{\infty }} u_k(x)dx={\textstyle \sum_{k=1}^{\infty }} \int_{a}^{b}u_k(x)dx$ （条件： ${\textstyle \sum_{n=1}^{\infty }} u_n(x)$ 一致收敛且每一项都连续）
$g'\left(y\right)=\int_a^b\frac{\partial f\left(x,y\right)}{\partial y}\operatorname dx$ , 即有连续导函数（条件： ${\textstyle \sum_{n=1}^{\infty }} u_n(x)$ 点点收敛， ${\textstyle \sum_{n=1}^{\infty }} u_n'(x)$ ）一致收敛且每一项都连续）

note：
$\left|{\textstyle\sum_{k=1}^n}\sin kx\right|(\left|{\textstyle\sum_{k=1}^n\cos kx}\right|)\leq\frac1{\left|\sin{\displaystyle\frac x2}\right|}$
通常使用 $\int_a^xS'(x)dx=S(x)-S(a)$ 得到 $S(x)$

幂级数

收敛半径R: 敛散性的分界点为x=R，即 $\lim_{n\rightarrow\infty}\left|\frac{un+1}{u_n}\right|=1$ 时 $\left|x\right|$ 的取值
R的求法：

$\lim_{n\rightarrow\infty}\left|\frac{a_{n+1}}{a_n}\right|=l$ , 则 $R=\frac1l$
$\lim_{n\rightarrow\infty}\sqrt[n]{a_n}=l$ , 则 $R=\frac1l$

幂级数性质：

内闭一致性：对 $\forall0<b<R$ ，幂级数在 $\left[-b,b\right]$ 上一致收敛；若幂级数在右端点x=R（左端点x=-R）处收敛，则它在 $\left[0,R\right]$ ( $\left[-R,0\right]$ )上一致收敛
连续性：幂级数的和函数 $S(x)={\textstyle\sum_{n=0}^\infty}a_nx^n$ 在收敛区间上连续
$\int_0^xS(t)\operatorname dt={\textstyle\sum_{n=0}^\infty}\int_0^xa_nt^n\operatorname dt={\textstyle\sum_{n=0}^\infty}\frac{a_n}{n+1}x^{n+1}$
$S'(x)={\textstyle\sum_{n=0}^\infty}(a_nx^n)'={\textstyle\sum_{n=1}^\infty}na_nx^{n-1}$

泰勒级数

形式： $f(x)={\textstyle\sum_{n=0}^\infty}a_n{(x-x_0)}^n$ ，其中， $a_n=\frac1{n!}f^{(n)}(x_0)$ ,且 $x-x_0\in(-R,R)$
泰勒余项： $R_n(x)=a_{n+1}{(x-x_0)}^{n+1}=\frac1{(n+1)!}f^{(n+1)}(x+\theta(x-x_0)){(x-x_0)}^{n+1}$ , f(x)能展开为泰勒级数的充要条件是 $\lim_{n\rightarrow\infty}R_n(x)=0$
在0附近的泰勒展开：

$e^x={\textstyle\sum_0^\infty}\frac1{n!}x^n$
$\sin x={\textstyle\sum_{n=0}^\infty}{(-1)}^n\frac{x^{2n+1}}{(2n+1)!}$
$\cos x={\textstyle\sum_{n=0}^\infty}{(-1)}^n\frac{x^{2n}}{(2n)!}$
$arc\tan x={\textstyle\sum_{n=0}^\infty}{(-1)}^n\frac1{2n+1}x^{2n+1}$
$\ln(1+x)={\textstyle\sum_{n=0}^\infty}{(-1)}^n\frac{x^{n+1}}{n+1}$
${(1+x)}^a={\textstyle\sum_{n=0}^\infty}\begin{pmatrix}\alpha\\n\end{pmatrix}x^n$

note：
陌生的函数可以先积分转化为熟悉函数的形式，在此形式上泰勒展开，再求导得到原函数的泰勒展开

第十一章广义积分与含参变量的积分

广义积分

无穷积分

收敛定义： 若 $\lim_{A\rightarrow\infty}\int_a^Af(x)\operatorname dx$ 存在，则称无穷积分 $\int_a^\infty f(x)\operatorname dx$ 收敛
$\int_{-\infty}^\infty f(x)\operatorname dx=\int_{-\infty}^0f(x)\operatorname dx+\int_0^\infty f(x)\operatorname dx$ 当右端两个无穷积分都收敛时，左端才收敛
柯西收敛原理： 对任意 $\varepsilon$ , 存在 A，使得 $\left|\int_A^{A'}f(x)dx\right|<\varepsilon$
命题：若 $\int_a^\infty\left|f(x)\right|dx$ 收敛，则 $\int_a^\infty f(x)dx$ 收敛
收敛判别法：

比较判别：设f(x),g(x)在 $\lbrack a,\infty)$ 上有定义,且 $0\leq f(x)\leq g(x)$ ,则
(1) 由 $\int_a^\infty g(x)\operatorname dx$ 收敛可推出 $\int_a^\infty f(x)\operatorname dx$ 收敛
(2) 由 $\int_a^\infty f(x)\operatorname dx$ 发散可推出 $\int_a^\infty g(x)\operatorname dx$ 发散
比较判别的极限形式： $\lim_{x\rightarrow\infty}\frac{f(x)}{g(x)}=k$
(1) k=0,分母收敛则分子收敛
(2) $k=\infty$ 分母发散则分子发散
(3) k=l, $0<l<\infty$ 则分子与分母敛散性一致
迪利克雷判别法：对于 $\int_a^\infty f(x)g(x)\operatorname dx$ , 对一切 $A\geq a$ , 都有 $\int_a^Af(x)\operatorname dx$ 有界;且g(x)单调趋于零，则收敛
阿贝尔判别法: $\int_a^\infty f(x)\operatorname dx$ 收敛，且 $\int_a^\infty g(x)\operatorname dx$ 单调有界，则收敛

瑕积分

收敛定义： 若 $\lim_{\varepsilon\rightarrow0+0}\int_{a+\varepsilon}^bf(x)\operatorname dx$ 存在，则称以a为瑕点的瑕积分 $\int_a^bf(x)\operatorname dx$ 收敛
若a，b均为瑕点，则 $\int_a^bf(x)\operatorname dx=\lim_{\varepsilon\rightarrow0+0}\int_{a+\varepsilon}^cf(x)\operatorname dx+\lim_{\eta\rightarrow0+0}\int_c^{b-\eta}f(x)\operatorname dx$ 右端两式均收敛则左端收敛
若a为瑕点，且是无穷积分，则 $\int_a^\infty f(x)dx=\int_a^cf(x)\operatorname dx+\int_c^\infty f(x)\operatorname dx$ 右端两式均收敛则左端收敛
柯西收敛原理： $\left|\int_{a+\delta_1}^{a+\delta_2}f(x)\operatorname dx\right|<\varepsilon$
命题：若 $\int_a^b\left|f(x)\right|dx$ 收敛,则 $\int_a^bf(x)dx$ 收敛
收敛判别法：

比较判别：f(x)和g(x)均以a为瑕点，且 $0\leq f(x)\leq g(x)$ ，则
(1) 由 $\int_a^bg(x)\operatorname dx$ 收敛可推出 $\int_a^bf(x)\operatorname dx$ 收敛
(2) 由 $\int_a^bf(x)\operatorname dx$ 发散可推出 $\int_a^bg(x)\operatorname dx$ 发散
比较判别的极限形式： $\lim_{f(x)\rightarrow a+0}\frac{f(x)}{g(x)}=k$
(1) k=0,分母收敛则分子收敛
(2) $k=\infty$ 分母发散则分子发散
(3) k=l, $0<l<\infty$ 则分子与分母敛散性一致
迪利克雷判别： $\int_a^bf(x)g(x)\operatorname dx$ ， a为瑕点，若 $\int_A^bf(x)dx$ 有界， $a<A<b$ ，且g(x)在 $x\rightarrow a$ 时单调趋近于0，则收敛
阿贝尔判别：若 $\int_a^bf(x)dx$ 收敛，g(x)单调有界，则收敛

note：

在使用比较判别法时，常用到以下典型瑕积分：
$\int_a^b{(\frac1{x-a})}^pdx$ 或 $\int_a^b{(\frac1{b-x})}^pdx$
其中， $p\geq1$ 时发散，p<1时收敛
常用洛必达法则判断某点是否为瑕点，如果该点有极限则不是瑕点

含参变量的正常积分

连续性： f(x,y)在R上连续时，g(y)在[c,d]上也连续，故有 $\lim_{y\rightarrow y_0}g(y)=g(y_0)$ ,即 $\lim_{y\rightarrow y_0}\int_a^bf(x,y)\operatorname dx=\int_a^bf(x,y_0)\operatorname dx=\int_a^b\lim_{y\rightarrow y_0}f(x,y)\operatorname dx$
可积性： f(x,y)在R上连续时， $\int_c^ddy\int_a^bf(x,y)dx=\int_a^bdx\int_c^df(x,y)dy$
可微性： f(x,y)在R上连续时， $\frac d{dy}\int_a^bf(x,y)\operatorname dx=\int_a^bf_y(x,y)\operatorname dx$ ,
当 $g(y)=\int_{u(y)}^{v(y)}f(x,y)\operatorname dx$ 时， $g'(y)=\int_{u(y)}^{v(y)}f_y(x,y)\operatorname dx+f(v(y),y)v'(y)-f(u(y),y)u'(y)$

含参变量的广义积分

一致收敛定义： $g(y)=\int_a^\infty f(x,y)\operatorname dx$ , 总存在A，使得， $\left|\int_A^\infty f(x,y)\operatorname dx\right|<\varepsilon$ 则g(y)一致收敛。
则当 $\left|\int_A^\infty f(x,y)\operatorname dx\right|>l$ (l>0), 或 $\lim_{y\rightarrow y_0}\int_A^\infty f(x,y)\operatorname dx=k\neq0$ 时，无穷积分不一致收敛
一致收敛判别法：

比较判别：若 $\left|f(x,y)\right|\leq\varphi(x)$ ,且 $\int_0^\infty\varphi(x)\operatorname dx$ 收敛，则g(y)一致收敛
迪利克雷判别：当 $x\rightarrow\infty,\;g(x,y)=0$ 且 $\left|\int_a^Af(x,y)\operatorname dx\right|\leq M$ , 则 $\int_a^\infty f(x,y)g(x,y)dx$ 一致收敛
阿贝尔判别：当g(x,y)关于x单调且有界， $\int_a^\infty f(x,y)\operatorname dx$ 一致收敛 ,则 $\int_a^\infty f(x,y)g(x,y)dx$ 一致收敛

一致收敛性质：

$\int_c^dg(y)\operatorname dy=\int_c^ddy\int_a^\infty f(x,y)\operatorname dx=\int_a^\infty dx\int_c^df(x,y)\operatorname dy$ (条件：g(y)一致收敛)
$\int_c^dg(y)\operatorname dy=\int_c^ddy\int_a^\infty f(x,y)\operatorname dx=\int_a^\infty dx\int_c^df(x,y)\operatorname dy$ (条件：g(y)点点收敛， $\int_a^\infty\frac{\partial f(x,y)}{\partial y}\operatorname dx$ 一致收敛)

$\Gamma$ 函数与B函数

$\Gamma$ 函数:

$\Gamma(\alpha)=\int_0^\infty x^{\alpha-1}e^{-x}\operatorname dx$
$\Gamma(n+1)=n\Gamma(n)=...=n!$
$\Gamma(\frac12)=\sqrt\pi$

B函数：

$B(p,q)=\int_0^1x^{p-1}{(1-x)}^{q-1}\operatorname dx$
B(p,q)=B(q,p)
$B(p,q)=\frac{\Gamma(p)\cdot\Gamma(q)}{\Gamma(p+q)}$

note：
$\int_0^\infty\frac{\sin\alpha x}x\operatorname dx=\left\{\begin{array}{l}\frac{\mathrm\pi}2,\alpha>0\\0,\alpha=0\\-\frac\pi2,\alpha<0\end{array}\right.$
$\int_0^\frac{\mathrm\pi}2\cos^m\theta\sin^n\theta\operatorname d\theta=\frac12B(\frac{m+1}2,\frac{n+1}2)$

第十二章傅里叶级数

三角函数系及其正交性

基本三角函数系： $1,\cos x,\sin x,...,\cos nx,\sin nx,...$
正交性：在基本三角函数系中任意两个不同函数的乘积在 $\lbrack-\pi,\pi\rbrack$ 上的积分为0

傅里叶级数及收敛性定理

设f(x)是一个以 $2\pi$ 为周期的函数，则

$f(x)=\frac{a_0}2+\sum_{n=1}^\infty(a_n\cos nx+b_n\sin nx)$
其中，
$a_0=\frac1\pi\int_{-\pi}^\pi f(x)\operatorname dx$
$a_n=\frac1\pi\int_{-\pi}^\pi f(x)\cos nx\operatorname dx$
$b_n=\frac1\pi\int_{-\pi}^\pi f(x)\sin nx\operatorname dx$

设f(x)是一个以T为周期的函数，则

$f(x)=\frac{a_0}2+\sum_{n=1}^\infty(a_n\cos\frac{n\pi}lx+b_n\sin\frac{n\pi}lx)$
其中，令 $l=\frac T2$
$a_0=\frac1l\int_{-l}^lf(x)\operatorname dx$
$a_n=\frac1l\int_{-l}^lf(x)\cos nx\operatorname dx$
$b_n=\frac1l\int_{-l}^lf(x)\sin nx\operatorname dx$
迪利克雷定理: $S(x)=\left\{\begin{array}{l}f(x)\\\frac{f(x+0)+f(x-0)}2\end{array}\right.$
note:

注意f(x)的奇偶性，当f(x)是偶函数时， $b_n=0$ ,当f(x)是奇函数时， $a_n=0$
若是展开成余弦级数，则将f(x)进行偶延拓( $b_n=0$ )，若是展开成正弦函数，则将f(x)进行奇延拓 ( $a_n=0$ )

帕塞瓦尔等式

$\frac{a_0^2}2+\sum_{k=1}^\infty(a_k^2+b_k^2)=\frac1\pi\int_{-\pi}^\pi f^2(x)\operatorname dx$ ，可用于求某些级数

完结撒花ovo！!